问题
证明题
求证:全等三角形的对应角平分线相等.
答案
已知:△ABC≌△ A'B'C',AD平分∠BAC,A'D'平分∠B'A'C'.
求证:AD=A'D'.
证:∵△ABC≌△A'B'C'.
∴∠B=∠B',AB=A'B'. ∠BAC=∠B'A'C'.
∵AD平分∠BAC,A'D'平分∠B'A'C'.
∴∠BAD=B'A'D'.
∴△ABD≌△A'B'D'.
∴AD=A'D'.
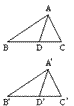
求证:全等三角形的对应角平分线相等.
已知:△ABC≌△ A'B'C',AD平分∠BAC,A'D'平分∠B'A'C'.
求证:AD=A'D'.
证:∵△ABC≌△A'B'C'.
∴∠B=∠B',AB=A'B'. ∠BAC=∠B'A'C'.
∵AD平分∠BAC,A'D'平分∠B'A'C'.
∴∠BAD=B'A'D'.
∴△ABD≌△A'B'D'.
∴AD=A'D'.
