问题
填空题
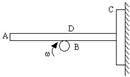
如图所示,重为G的均匀棒水平地搁在一个圆柱体B上.二者的接触点D离棒的左端距离是棒长的3/5,当圆柱体顺时针方向转动时,在棒的右端与它紧靠着的木板C恰能沿光滑竖直墙面匀速下滑,则木板C的重为______.若木棒与圆柱体间的动摩擦因素为μ,则棒与圆柱体间的滑动摩擦力为______.
答案
因为棒均匀,令棒长为L,c对棒的摩擦力为f,则重力在
处,以D为支点棒满足力矩平衡,有:L 2
G•(
L-3 5
)=f•(L-L 2
L)3 5
可解得f=G 4
以C为研究对象,因为C匀速下降,故C处于平衡状态,棒对C的摩擦力等于C的重力
根据牛顿第三定律可得:GC=f=G 4
(2)以棒为研究对象,在竖直方向受重力、C对棒竖直向下的摩擦力f和B对D点竖直向上的弹力N作用,根据平衡可得:
G+f=N
所以N=G+f=5G 4
所以棒与圆柱体间的滑动摩擦力f滑=μN=μ5G 4
故答案为:
,G 4 μ5G 4
