如图甲所示,平行金属导轨间距为L1=0.5m,导轨平面与水平面间的夹角θ=30°,两横截面为正方形、质量均为m=0.1kg的金属棒ab、cd垂直导轨静止在导轨平面上,两棒之间的距离L2=0.4m,两棒与导轨间的动摩擦因数均为μ=
,两棒在导轨之间部分的电阻均为R=0.1Ω,导轨电阻不计.现将整个装置置于垂直于轨道平面向上的匀强磁场中,磁感应强度随时间的变化关系如图乙所示.设两棒与导轨问的最大静摩擦力均等于滑动摩擦力,两棒横截面的边长远小于它们之间的距离,忽略两棒上电流之间的相互作用,g取10m/s2.3 2
(1)两金属棒都未出现滑动之前,闭合回路中的电流多大?金属棒ab中电流方向如何?
(2)哪个金属棒先发生滑动?是在哪一时刻?
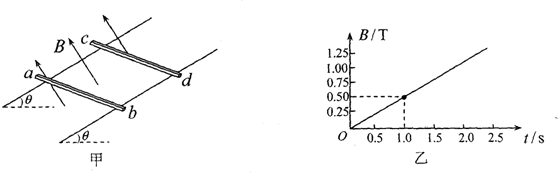
(1)由图可知,磁感应强度的变化率为:
=0.5T/s△B △t
感应电动势E=
L1L2,△B △t
I=E 2R
由以上等式解得:I=0.5A.
由楞次定律判断电流方向为:由b到a.
(2)对ab、cd进行受力分析,ab所受安培力沿斜面向上,cd所受安培力沿斜面向下,
由于ab、cd的重力沿斜面向下的分力小于它们与斜面的最大静摩擦力,
所以金属棒cd先发生滑动,
F安=BIL1,
F安+mgsinθ=μmgcosθ
B=
t△B △t
由以上等式解得:t=2s.
答:(1)两金属棒都未出现滑动之前,闭合回路中的电流为0.5A,金属棒ab中电流方向由b到a.
(2)t=2s,金属棒cd先发生滑动.
