如图所示,AB、CD分别是两个可以绕A、C两转轴转动的质量均匀的杠杆,它们的质量相等,长度相等.现在B端施加一个始终垂直AB杆的力,使AB杆和CD杆缓缓绕顺时针或逆时针转动.设使AB杆顺时针转动到图示位置时施加在B点的力为F1,使AB杆逆时针转动到图示位置时施加在B点的力为F2.则下列说法中正确的是( )
A.若CD杆与AB杆接触处是光滑的,则F1<F2
B.若CD杆与AB杆接触处是光滑的,则F1>F2
C.若CD杆与AB杆接触处是有摩擦的,则F1<F2
D.无论接触点是否光滑,及转动方向如何,F1=F2
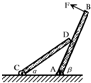
(1)若CD杆与AB杆接触处是光滑的.
AB杆上的B为支点,作用在AB杆上的力有:F、重力G、CD杆对AB杆的压力F′,
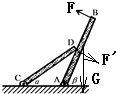
则根据杠杆平衡条件得:
F•L1=G•L2+F′•L3,
无论AB杆顺时针转动还是逆时针转动,F的力臂L1、AB杆的重力G及重力力臂L2、压力F′及力臂L3都不变,所以,
F1=F2.

(2)若CD杆与AB杆接触处是有摩擦的.
AB杆受力F,G,F′,摩擦力f,力矩为
顺时针转动:F1•L1=G•L2+F1′•L3+f1•0---------------①
逆时针转动:F2•L1=G•L2+F2′•L3+f2•0---------------②
∵CD杆对AB杆的压力F′在两种情况中不同,
①顺时针转动时,
CD杆受力:有G、F1″、f1′,摩擦力f1′方向沿AB杆向上,μ为CD杆与AB杆之间的摩擦系数,
则:F1″•L4+f1′•L6=G•L5,即:F1″•L4+μ•F1″•L6 =G•L5,
∴F1″=GL5 L4+μL6

②逆时针转动时,
CD杆受力也是有G,F2″,f2′,但摩擦力f2′方向沿AB杆向下,
则:F2″•L4=G•L5+f2′•L6,
即:F2″•L4=G•L5+μ•F2″•L6
∴F2″=GL5 L4-μL6
∵CD杆上的G、L4、L5、μ、L6 都不变,
∴F1″<F2″
∵F1′与F1″,F2′与F2″是一对相互作用力,
∴F1′<F2′-----------③.
代入前面的①②式比较可得:
F1<F2.
故选C.
