问题
选择题
如图所示,A、B两球完全相同,质量均为m,用两根等长的细线,悬挂在升降机的天花板上的O点,两球之间连着一根劲度系数为k的轻质弹簧.当升降机以加速度a竖直向上加速运动时,两根细线之间的夹角为θ.则弹簧的长度与原长相比缩短了( )
A.m(a+g)tanθ k
B.mgtanθ k
C.m(a+g)tan θ 2 k
D.2m(a+g)tan θ 2 k 
答案
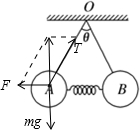
对球A受力分析,受重力mg、拉力T、弹簧的弹力F而向上做匀加速直线运动,如图
则有牛顿第二定律可知:
-mg=maF tan θ 2
即:F=(g+a)tanθ 2
根据胡克定律,有
F=kx
解得
x=m(a+g)tan θ 2 k
故选:C.
