问题
问答题
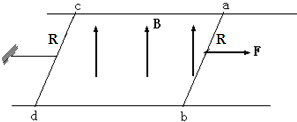
如图所示,在方向竖直向上、磁感应强度为B的匀强磁场中,有两条光滑的平行金属导轨,其电阻不计,间距为L,导轨平面与磁场方向垂直,ab、cd为垂直放置在导轨上的两根相同的金属棒,它们的电阻都为R、质量都为m,abdca构成闭合回路,cd棒用能承受最大拉力为FT的水平细线拉住,ab棒在水平拉力F的作用下以加速度a由静止开始向右做匀加速运动.
求:(1)经多长时间细线将被拉断;
(2)细线被拉断前,F随时间t的变化规律;
(3)从ab棒开始运动到cd棒刚要开始运动的过程中,流过cd棒的电荷量.
答案
(1)设经t时间细线将被拉断,此时棒ab产生的感应电动势为 E=BLv=BLat,
回路中感应电流为I=
,E 2R
cd棒所受的安培力为 F安=BIL=
t=FT,B2L2a 2R
解得 t=2RFT B2L2a
(2)细线被拉断前,对ab棒,由牛顿第二定律得
F-BIL=ma,所以F=
t+maB2L2a 2R
(3)从ab棒开始运动到cd棒刚要开始运动的过程中,由
=. E
,I=△Φ △t
,q=. E 2R
△t得. I
q=
=△φ 2R BL•
at21 2 2R
将t=
代入得 q=2RFT B2L2a R(FT)2 B3L3a
答:
(1)经
时间细线将被拉断;2RFT B2L2a
(2)细线被拉断前,F随时间t的变化规律为:F=
t+ma;B2L2a 2R
(3)从ab棒开始运动到cd棒刚要开始运动的过程中,流过cd棒的电荷量为
.R(FT)2 B3L3a
