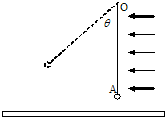
如图所示,一矩形轻质柔软反射膜可绕过O点垂直纸面的水平轴转动,其在纸面上的长度为L1,垂直纸面的长度为L2.在膜的下端(图中A处)挂有一平行于转轴,质量为m,长为L3的导体棒使膜形成平面.在膜下方水平放置一足够大的太阳能光电池板,能接收到经反射膜反射到光电池板上的所有光能,并将其转化成电能.光电池板可等效为一个电池,输出电压恒定为U;输出电流正比于光电池板接收到的光能(设垂直于入射光单位面积上的光功率保持恒定).导体棒处在方向竖直向上的匀强磁场B中,并与光电池构成回路,流经导体棒的电流垂直纸面向外(注:光电池与导体棒直接相连,连接导线未画出).
(1)再有一束平行光水平入射,当反射膜与竖直方向成θ=60°时,导体棒受力处于平衡状态,求此时电流强度的大小和光电池的输出功率.
(2)当θ变成45°时,光电池板接收到的光能对应的功率P’与当θ=60°时光电池板接收到的光能对应的功率P之比?
(3)当θ变成45°时,通过调整电路使导体棒保持平衡,光电池除维持导体棒处于平衡外,还能输出多少额外电功率?
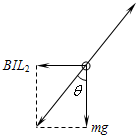
(1)导体棒受力如图,棒所受的安培力FA=BIL2,导体棒受力平衡,则有
mgtanθ=FA,
解得,I=
当θ=60°时,I1=
光电池输出功率为P1=UI1=.
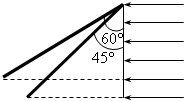
(2)当θ变成45°时,设光电池输出功率为P2,根据几何关系可知:==
(3)当θ=45°时,维持力平衡需要的电流为I2=,可得P2=P1=
而光电池产生的电流为I光电==,所以能提供的额外电流为I额外=I光电-I2=(-1)
故可提供额外功率为P额外=UI额外=.
答:
(1)此时电流强度的大小是,光电池的输出功率是.
(2)当θ变成45°时,光电池板接收到的光能对应的功率P′与当θ=60°时光电池板接收到的光能对应的功率P之比为.
(3)还能输出额外电功率为.