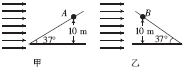
两根完全相同的光滑细直杆上各套有一个完全相同的小球，且两杆均与水平面成37°角放置，将两小球均从离地面10m高处由静止释放，如图甲、乙所示．在水平向右的风力作用下，A球保持静止，B球沿细直杆下滑．求B球滑到地面所需的时间．（结果保留三位有效数字）（sin37°=0.6，cos37°=0.8）
设风力大小为F．对A受力分析后，由平衡条件得
mgsin37°-Fcos37°=0
解得，风力F=mgtan37°
对B受力分析，由牛顿第二定律得
mgsin37°+Fcos37°=ma
解得，a=2gsin37°=12m/s2
又s=
at2，1 2
由几何关系得，s=h sin37°
联立得，
=h sin37°
at21 2
解得，t≈1.67s
答：B球滑到地面所需的时间是1.67s．
| 2008年长三角部分城市国内生产总值情况表 | |||||||
| 城市 | 国内生产总值 (亿元) | 第一产业 (亿元) | 同比增长 (%) | 第二产业 (亿元) | 同比增长 (%) | 第三产业 (亿元) | 同比增长 (%) |
| 上海市 | 13698.15 | 111.8 | 0.7 | 6235.92 | 8.2 | 7350.43 | 11.3 |
| 南京市 | 3775 | 93 | 13 | 1795 | 9.6 | 1887 | 15.3 |
| 扬州市 | 1573.29 | 117.47 | 5 | 897.71 | 13.8 | 558.11 | 14.5 |
| 南通市 | 2510.13 | 199.18 | 4.1 | 1430.93 | 13.7 | 880.02 | 15.0 |
| 杭州市 | 4781.16 | 178.64 | 3.6 | 2389.4 | 9.O | 2213.1 | 13.8 |
| 宁波市 | 3964.05 | 167.4 | 4.1 | 2196.68 | 10.0 | 1600.01 | 11.0 |
| 嘉兴市 | 1815.30 | 105.52 | 2.3 | 1085.29 | 10.5 | 624.49 | 12.5 |
表中七个城市2008年的国内生产总值之和与以下哪个最接近
A．3.2万亿元
B．3.4万亿元
C．3.6万亿元
D．3.8万亿元