问题
问答题
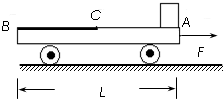
如图所示，光滑水平地面上停着一辆平板车，其质量为2m，长为L，车右端（A点）有一块静止的质量为m的小金属块．金属块与车间有摩擦，以中点C为界，AC段与CB段摩擦因数不同．现给车施加一个向右的水平恒力，使车向右运动，同时金属块在车上开始滑动，当金属块滑到中点C时，撤去这个力．已知撤去力的瞬间，金属块的速度为v0，车的速度为2v0，最后金属块恰好停在车的左端（B点）．如果金属块与车的AC段间的动摩擦因数为μ1，与CB段间的动摩擦因数为μ2，求μ1与μ2的比值．
答案
金属块由A→C过程中做匀加速运动，加速度为：
a1=
=f m
=μ1g μ1mg m
设金属块由A到达C历时为t1，速度v0=a1t1…①
小车加速度a2=2a1=2μ1g．
车此刻的速度：2v0=a2t1…②
金属块与小车位移之差：s=
a2t12-1 2
a1t12=1 2
(2μ1g-μ1g)(1 2
)2，v0 μ1g
而s=
，L 2
所以：μ1=
…③v02 gL
从小金属块滑至车中点C开始到小金属块停在车的左端，它与车有共同速度，设为v，此过程中，系统水平方向动量守恒，有
2m×2v0+mv0=（2m+m）v，
得v=
v0． 5 3
此过程中系统动能损失为μ2mg
=L 2
mv02+1 2
×2m×(2v0)2-1 2
×3m×(1 2
v0)2，5 3
解得：μ2=
…④2v02 3gL
得：③ ④
=μ1 μ2
． 3 2
答：μ1与μ2的比值为3：2．
