问题
问答题
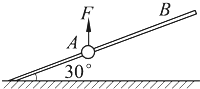
如图所示,一重为10N的小球,在F=20N的竖直向上的拉力作用下,从A点由静止出发向上运动,F作用1.2s后撤去,已知杆与球间的动摩擦因数为
,试求从撤去力F开始计时,小球经多长时间将经过距A点为2.25m的B点.(g=10m/s2)3 6
答案
在力F作用时有:
(F-mg)sin30°-m(F-mg)cos30°=ma1
a1=2.5 m/s2
刚撤去F时,小球的速度v1=a1t1=3m/s
小球的位移s1 =
t1=1.8m v1 2
撤去力F后,小球上滑时有:
mgsin30°+μmgcos30°=ma2
a2=7.5 m/s2
因此小球上滑时间t2=
=0.4s 上滑位移s2=v1 a2
t2=0.6mv1 2
则小球上滑的最大距离为sm=s1+s2=2.4m
撤除F到B点位移△s=sB-s1
设时间为t
△S=vt-
a2t21 2
解得t=0.2s或t=0.6s(舍去)因为小球上升到最高点返回时的加速度不再等于a2.
小球匀减速直线运动到零的位移x=
=0.6m 减速到零的时间t″=v2 2a2
=v a2
s=0.4s3 7.5
返回到B点的位移x′=0.6-0.45m=0.15m
根据牛顿第二定律得,mgsin30°-μmgcos30°=ma3
解得a3=2.5m/s2
根据x′=
a3t′2,解得t′=1 2
s3 5
则t=t′+t″=0.4+
s=0.75s3 5
答:若从撤去力F开始计时,小球经0.2s或0.75s经过距A点上方为2.25m的B点.
