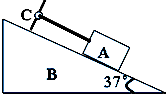
将质量为1kg的物块A用一轻杆拴在质量为2kg的倾角为37°的斜面B上,轻杆与斜面平行,如图所示,C是铰链,杆可绕C点转动,所有接触面光滑,(g=10m•s-2)求:
(1)当给斜面水平向左的拉力为40N时,求杆对A的作用力和B对A的支持力
(2)当物体以加速度大小为10m•s-2的加速度沿水平方向运动时,求杆对A的作用力和B对A的支持力
(3)请你再提两个有关物块A运动的物理问题(不要求论证、计算).
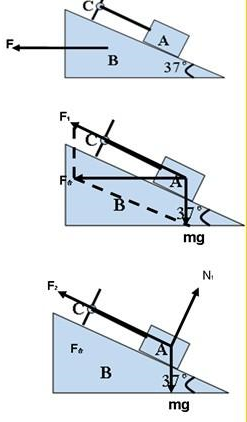
(1)把系统看成整体,根据牛顿第二定律得:
a=
=F m
m/s240 3
以A为研究对象,当A仅受杆对A的拉力和重力时,有:
a′=gcot37°=
m/s240 3
a=a′所以恰好满足临界条件B对A没有支持力,
F1=
≈16.67Nmg sin37°
(2)当物体向左加速运动,10m/s2<
m/s240 3
所以B对A有支持力,如图所示,沿斜面正交分解,
F2-mgsin37°=macos37°
mgcos37°-N1=masin37°
解得:F2=14N,N1=2N
当物体向右加速运动,10m/s2>7.5m/s2
所以杆对A也有力的作用,
F3+mgsin37°=macos37°
N2-mgcos37°=masin37°
解得:N2=14N,F3=2N
(3)①求绳子断开瞬间物块A的加速度,②力作用3s后撤去,则物体能滑行多远.
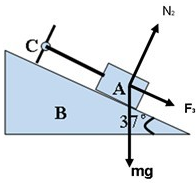
答:(1)当给斜面水平向左的拉力为40N时,杆对A的作用力为16.67N,B对A的支持力为0;
(2)当物体以加速度大小为10m•s-2的加速度沿水平方向运动时,杆对A的作用力为14N或2N,B对A的支持力为2N或14N;
(3)①求绳子断开瞬间物块A的加速度,②力作用3s后撤去,则物体能滑行多远.

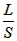 ,式中R表示导线的电阻,L表示导线的长度,S表示导线的横截面积,ρ是导线材料的电阻率。导线的材料不同,ρ的大小一般也不同,由公式R=p
,式中R表示导线的电阻,L表示导线的长度,S表示导线的横截面积,ρ是导线材料的电阻率。导线的材料不同,ρ的大小一般也不同,由公式R=p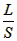 ,可以得出ρ=
,可以得出ρ=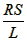 。
。