如图为一个小型交流发电机的原理图,其矩形线圈的面积为S,共有n匝,线圈总电阻为r,可绕与磁场方向垂直的固定对称轴OO′转动;线圈处于磁感应强度为B的匀强磁场中,线圈在转动时可以通过滑环K和电刷L保持与外电路电阻R的连接.在外力作用下线圈以恒定的角速度ω绕轴OO′匀速转动.(不计转动轴及滑环与电刷的摩擦)
(1)推导发电机线圈产生感应电动势最大值的表达式Em=nBSω;
(2)求线圈匀速转动过程中电流表的示数;
(3)求线圈速度转动N周过程中发电机线圈电阻r产生的焦耳热.
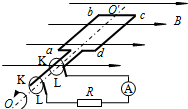
(1)线圈平面与磁场方向平行时产生感应电动势最大,设ab边的线速度为v,该边产生的感应电动势为:E1=BLabv
与此同时,线圈的cd边也在切割磁感线,产生的感应电动势为:E2=BLcdv
线圈产生的总感应电动势为:Em=n(E1+E2)
因为有:Lab=Lcd,
所以:Em=n2BLabv
线速度v=ω
Lbc,所以:Em=nBLabLbcω,而S=LabLbc(S表示线圈的面积)1 2
Em=nBSω;
(2)线圈匀速转动过程中电流表的示数是有效值,所以感应电动势的有效值是nBSω 2
根据闭合电路的欧姆定律得I=
=E r+R 2 2
.nBSω R+r
所以电流表的示数是2 2
.nBSω R+r
(3)线圈匀速转动的周期是T=2π ω
根据焦耳定律得:
线圈速度转动N周过程中发电机线圈电阻r产生的焦耳热Q=I2r×NT=
.πNn2B2S2ωr (r+R)2
答:(1)见解答(1);
(2)线圈匀速转动过程中电流表的示数是2 2
;nBSω R+r
(3)线圈速度转动N周过程中发电机线圈电阻r产生的焦耳热是
.πNn2B2S2ωr (r+R)2
