已知一足够长的传送带与水平面的倾角为θ，以一定的速度匀速运动

问题选择题

已知一足够长的传送带与水平面的倾角为θ，以一定的速度匀速运动．某时刻在传送带适当的位置放上具有一定初速度的物块（如图a所示），以此时为t=0时刻纪录了小物块之后在传送带上运动的速度随时间的变化关系，如图b所示（图中取沿斜面向上的运动方向为正方向，其中两坐标大小v₁＞v₂）．已知传送带的速度保持不变，g取10m/s²．则下列判断正确的是（　　）

A．0～t₁内，合外力对物块做功为W=-

mv12

B．物块与传送带间的动摩擦因数为μ，μ＜tanθ

C．0～t₁内，传送带对物块做正功

D．0～t₂内，传送带对物块做功为W=

2mv22-

mv12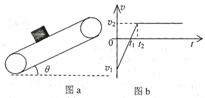

答案

A、0～t₁内，根据动能定理得：合外力对物块做功为W=0-

．故A正确．

B、由图看出，在t₁～t₂内，物块向上加速运动，则有 μmgcosθ＞mgsinθ，得μ＞tanθ．故B错误．

C、0～t₁内，物块向下运动，传送带向上运动，物块所受的滑动摩擦力方向沿斜面向上，与速度方向相反，则传送带对物块做负功．故C错误．

D、0～t₂内，由图“面积”等于位移可知，物块的总位移沿斜面向下，高度下降，重力对物块做正功，设为W_G，根据动能定理得：W+W_G=

mv22-

mv12，

则传送带对物块做功W=

mv22-

mv12-W_G．故D错误．

故选A