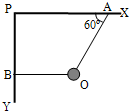
如图所示,XPY为直角支架,两根细绳的一端都拴在重物O上,另一端分别固定于支架的A、B两点.开始时,杆PX、绳OB水平,杆PY竖直,绳OA与水平方向夹角为60°.现使支架绕过P的水平轴在竖直平面内顺时针方向缓慢转动至杆PY水平,在上述过程中,绳OA、OB的拉力FA、FB的变化情况是( )
A.FA减小,FB先减小后增大
B.FA减小,FB先增大后减小
C.FA先减小后增大,FB增大
D.FA先增大后减小,FB增大
选取水平和竖直方向正交分解,设OB与水平方向夹角为α
当α≤60°时
则水平方向FBcosα=FAcos(60°-α)
竖直方向FBsin(60°-α)+FAsinα=mg
解得FA=mgcosα sin60°
FB=mgcos(60°-α) sin60°
此过程中随α的增大 FA减小 FB增大
当α≥60°时
则水平方向FBcosα=FAcos(α-60°)
竖直方向FBsinα=FAsin(α-60°)+mg
解得FA=mgcosα sin60°
FB=
,此过程中随α的增大 FA减小 FB增大减小mgcos(α-60°) sin60°
当α=90°时,FA=0.故B正确,A、C、D错误.
故选B.

