（16分）如图所示，在倾角θ＝30º的斜面上放置一段凹槽B，B与斜面间的动摩擦因数μ＝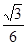
，槽内靠近右侧壁处有一小球A，它到凹槽内左壁侧的距离d＝0.10m．A、B的质量都为m=2.0kg，B与斜面间的最大静摩擦力可认为等于滑动摩擦力，不计A、B之间的摩擦，斜面足够长．现同时由静止释放A、B，经过一段时间，A与B的侧壁发生碰撞，碰撞过程不损失机械能，碰撞时间极短．取重力加速度g=10m/s2．求：
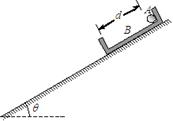
（1）A与B的左侧壁第一次发生碰撞后瞬间A、B的速度．
（2）在A与B的左侧壁发生第一次碰撞后到第二次碰撞前的这段时间内，A与B的左侧壁的距离最大可达到多少？
（1）A、B的速度分别为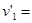
0，
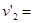1.0 m/s（方向沿斜面向下）（2）A与B的左侧壁的距离最大可达到0.10m
题目分析：（1）A在凹槽内，B受到的滑动摩擦力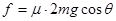
="10N" ，B所受重力沿斜面的分力
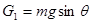="10N" ， 因为
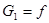，所以B受力平衡，释放后B保持静止（1分）
释放A后，A做匀加速运动，由牛顿定律和运动学规律得：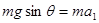
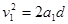（1分）
（1分）
解得A的加速度和碰撞前的速度分别为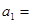
5m/s2，
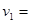1.0 m/s （1分）
A、B发生碰撞，动量守恒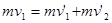 
（1分）
碰撞过程不损失机械能，得 
（1分）
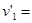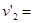解得A、B的速度分别为0，1.0 m/s（方向沿斜面向下） （2分）
（2）A、B第一次碰撞后，B做匀速运动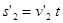 
（1分）
A做匀加速运动，加速度仍为a1
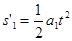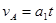（1分）
（1分）
经过时间t1，A的速度与B相等，A与B的左侧壁距离达到最大，即
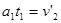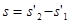（1分）
（1分）
代入数据解得A与B左侧壁的距离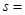
0.10m （1分）
因为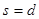
， A恰好运动到B的右侧壁，而且速度相等，所以A与B的右侧壁恰好接触但没有发生碰撞。
因此A与B的左侧壁的距离最大可达到0.10m。 （2分）
点评：本题难度中等，明确题目所给的碰后速度相同的条件，通过分析受力和做功情况判断运动和能量变化情况，判断出速度相同是两者距离最大的临界条件是本题求解的关键