问题
问答题
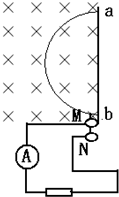
如图所示,一个半径为L的半圆形线圈,以直径ab为轴匀速转动,转速为n,ab的左侧有垂直纸面向里(与ab垂直)的匀强磁场,磁感应强度为B,M和N是两个集流环,负载电阻为R线圈、电流表和连接导线的电阻不计,求:
(1)电流表的示数;
(2)从图示位置起转过1/4周期内负载电阻R上产生的热量;
(3)从图示位置起转过1/4周期内负载电阻R的电荷量.
答案
(1)因最大感应电动势,则有:Em=BSω,
又闭合电路欧姆定律,则有:Im=
;Em R
电流的有效值,I=
=Im 2
=Em
R2
=BωS
R2
=B×2πn×
πL21 2
R2 π2L2nB
R2
因只存在左侧匀强磁场,因此电流表的示数,I′=
;π2L2nB
R2
(2)根据焦耳定律,则有,
从图示位置起转过
圈的时间内负载电阻R上产生的热量为Q=I2Rt=(1 4
)2R×π2L2nB
R2
=(T 4
)2R×π2L2nB
R2
×1 4
=2π 2πn π4B2L4n 8R
(3)从图示位置起转过
圈的时间内,穿过线框平面的磁通量的变化量为:△∅=B1 4
πL2.1 2
根据推论得到,通过通过小灯泡的电荷量为q=
•△t=. I
•△t=. E R
△t=△∅ △t R
=△∅ R πBL2 2R
答:(1)电流表的示数,I=
;π2L2nB
R2
(2)从图示位置起转过
周期内负载电阻R上产生的热量Q=1 4
;π4B2L4n 8R
(3)从图示位置起转过
周期内负载电阻R的电荷量q=1 4
.πBL2 2R
