问题
选择题
如图,一半圆形碗的边缘上装有一定滑轮,滑轮两边通过一不可伸长的轻质细线挂着两个小物体,质量分别为m1、m2,m1>m2.现让m1从靠近定滑轮处由静止开始沿碗内壁下滑.设碗固定不动,其内壁光滑、半径为R.则m1滑到碗最低点的速度为( )
A.2(m1-
m2)gR2 2m1+m2
B.2(m1-m2)gR m1+m2
C.2(m1-
m2)gR2 m1+m2
D.2(m1-m2)gR 2m1+m2 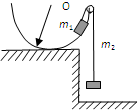
答案
设m1到达最低点时,m2的速度为v,则m1的速度v′=
=v cos45°
v.2
根据系统机械能守恒有:
m1gR-m2g.
R=2
m2v2+1 2
m1v′21 2
又v′=
v2
联立两式解得:v=
.所以v′=22(m1-
m2)gR2 2m1+m2
.(m1-
m2)gR2 2m1+m2
故选A.
