如图1所示,两根足够长、电阻不计的平行光滑金属导轨相距为L1=1m,导轨平面与水平面成θ=30°角,上端连接阻值R=1.5Ω的电阻;质量为m=0.2kg、阻值r=0.5Ω的金属棒ab放在两导轨上,距离导轨最上端为L2=4m,棒与导轨垂直并保持良好接触.整个装置处于一匀强磁场中,该匀强磁场方向与导轨平面垂直,磁感应强度大小随时间变化的情况如图2甲所示.一开始为保持ab棒静止,在棒上施加了一平行于导轨平面的外力F,已知当t=2s时,F恰好为零.求:
(1)当t=2s时,磁感应强度B的大小;
(2)当t=3s时,外力F的大小和方向;
(3)当t=4s时,突然撤去外力F,当金属棒下滑速度达到稳定时,导体棒ab两端的电压为多大;
(4)请在图2乙中画出前4s外力F随时间的变化情况.
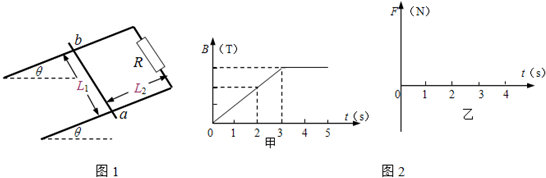

(1)回路中产生的感应电动势为E=
=L1L2△φ △t
=L1L2△B △t
,B2 2
感应电流为 I=
=L1L2E R+r
,B2 2(R+r)
在t=2s时刻,外力F=0,由平衡条件得
mg sin30°=B2IL1=L12L2
,B2 2(R+r)
可解得B2=1T,
(2)当t=3s时,由图可知B3=1.5 T,则由平衡条件得
外力F=B3IL1-mg sin30°=B3L12L2
-mg sin30°=0.5N,方向沿斜面向下B2 2(R+r)
(3)当t=4s时,突然撤去外力F,当金属棒下滑速度达到稳定时做匀速直线运动,则有
mg sin30°=BIL1,
解得,I=
=0.67 A,导体棒ab两端电压为 U=IR=1Vmgsin30° BL1
(4)在前3s内,由平衡条件得:
mg sin30°=BIL1+F,得F=mg sin30°-BIL1
而B=0.5t(T),I=L1L2
=1×4×B2 2(R+r)
A=1A,1 2(1.5+0.5)
得到F=1-0.5t
在t=3s后,B不变,则F不变.
作出图象如图.
答:
(1)当t=2s时,磁感应强度B的大小是1T;
(2)当t=3s时,外力F的大小是0.5N,方向沿斜面向下.
(3)当t=4s时,突然撤去外力F,当金属棒下滑速度达到稳定时,导体棒ab两端的电压为1V.
(4)画出前4s外力F随时间的变化情况如图.