如图甲所示,“目”字形轨道的每一短边的长度都等于a,只有四根平行的短边有电阻,阻值都是r,不计其它各边电阻.使导轨平面与水平面成夹角θ固定放置,如图乙所示.一根质量为m的条形磁铁,其横截面是边长为a的正方形,磁铁与导轨间的动摩擦因数为μ,磁铁与导轨间绝缘.假定导轨区域内的磁场全部集中在磁铁的端面,并可视为匀强磁场,磁感应强度为B,方向垂直导轨平面.开始时磁铁端面恰好与正方形3重合,现使其以某一初速度下滑,磁铁恰能匀速滑过正方形2,直至磁铁端面恰好与正方形1重合.已知重力加速度为g.求:

(1)上述过程中磁铁运动经历的时间;
(2)上述过程中所有电阻消耗的电能.
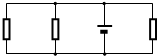
(1)设磁铁匀速进入正方形2的速度为v,等效电路如图所示.
感应电动势 E=Bav
总电阻 R=r+
=r 3
r4 3
感应电流 I=
=E R 3Bav 4r
切割磁感线的短边受到的安培力 F=BIa=3B2a2v 4r
短边受到的安培力与磁铁受到的力是作用力与反作用力
根据平衡条件 mgsinθ=F+f
滑动摩擦力 f=μ mgcosθ
解得:v=4mgr(sinθ-μcosθ) 3B2a2
当磁铁进入正方形1时,仍以速度v做匀速直线运动.
整个过程磁铁运动经历的时间 t=2a v
解得:t=3B2a3 2mgr(sinθ-μcosθ)
(2)根据能量守恒定律 mg•2asinθ=μ mg cosθ•2a+E
解得:E=2mga(sinθ-μ cosθ)
答:
(1)上述过程中磁铁运动经历的时间为
;3B2a3 2mgr(sinθ-μcosθ)
(2)上述过程中所有电阻消耗的电能为2mga(sinθ-μ cosθ).
