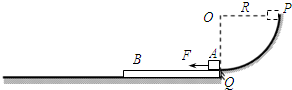
如图所示,一滑板B静止在水平面上,上表面所在平面与固定于竖直平面内、半径为R的1/4圆形光滑轨道相切于Q.一物块A从圆形轨道与圆心等高的P点无初速度释放,当物块经过Q点滑上滑板之后即刻受到大小F=2μmg、水平向左的恒力持续作用.已知物块、滑板的质量均为m,物块与滑板间的动摩擦因数μ=3μ,滑板与水平面间的动摩擦因数μ=μ,物块可视为质点,重力加速度取g.
(1)求物块滑到Q点的速度大小;
(2)简单分析判断物块在滑板上滑行过程中,滑板是否滑动;
(3)为使物块不从滑板上滑离,滑板至少多长?
(1)物块A从P点运动到Q点的过程中,由动能定理有:
mgR=
m1 2
-0v 21
解得:v1=2gR
(2)物块与滑板间的滑动摩擦力f1=μ1mg=3μmg
滑板与水平面间的滑动摩擦力f2=μ2(m+m)g=2μmg<f1
故物块在滑板上滑行的过程中,滑板将向左滑动.
(3)对于物块与滑板构成的系统,f2=F,系统动量守恒定律:
mv1=2mv
解得:v=2gR 2
设滑板的长度至少为L,物块与滑板共速前滑板滑行的位移为L1,对于系统由动能定理有:
F(L+L1)-f1((L+L1)+f1L1-f2L1=
2mv2-1 2
m1 2 v 21
解得:L=R 2μ
答:(1)物块滑到Q点的速度大小是
;2gR
(2)滑板将向左滑动;
(3)为使物块不从滑板上滑离,滑板至少R 2μ