问题
多选题
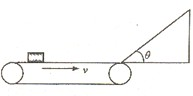
一水平传送带以2.0m/s的速度顺时针传动,水平部分长为2.0m.,其右端与一倾角为θ=37°的光滑斜面平滑相连,斜面长为0.4m,一个可视为质点的物块无初速度地放在传送带最左端,已知物块与传送带间动摩擦因数μ=0.2,则( )
A.物块能达斜面顶端
B.物块不能到达斜面顶端
C.物块最终静止在水平传送带右端
D.物块能返回到出发点
答案
物块在传送带上先做匀加速直线运动:
μmg=mal
al=2m/s2
当两者速度相等时,t=
=v a1
=1s2 2
此时物块运动的位移为:s1=
a1t2=1 2
×2×1m=1m<2m1 2
所以在到达传送带右端前物块已匀速,速度为2m/s
物块以ν0速度滑上斜面
-mgsinθ=ma2
a2=-6m/s2
物块速度为零时上升的距离
s2=
=0-v2 2a2
=0-4 -12
m1 3
由于s2<0.4m,所以物块未到达斜面的最高点.
物块上升的最大高度:
hm=s2sinθ=0.2m,故A错误,B正确;
物块返回皮带时滑的距离为x,则mghm-μmgx=0,x=1m,所以物块返回皮带时不会到达最左端,故D错误.
根据能量守恒可知,物块每次返回的距离逐渐变小,最终会停在最右端,故C正确.
故选BC
