问题
问答题
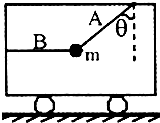
如图所示,在水平地面的车厢中,一小球被两根轻质细绳A、B栓住,其中A与竖直方向成θ角,B成水平状态,小球的质量为m,重力加速度为g,求:
(1)车厢静止时,细绳A和B所受的拉力.
(2)当车厢以一定的加速度运动时,A绳与竖直方向的夹角不变,而B绳受到的拉力为零,求此时车厢的加速度a1的大小和方向.
(3)若车厢向左以加速度a2匀加速运动时,求A、B两绳拉力的大小.
答案
(1)小球受重力两个拉力处于平衡,受力如图.
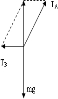
根据共点力平衡得,TA=
,TB=mgtanθ.mg cosθ
(2)当车厢以一定的加速度运动时,A绳与竖直方向的夹角不变,而B绳受到的拉力为零,对小球分析:
小球所受的合力水平向右,大小F合=mgtanθ.
则小球的加速度a=
=gtanθ.F合 m
所以车厢的加速度a1=gtanθ,方向水平向右.
(3)若车厢向左以加速度a2匀加速运动时,小球的加速度为a2.对小球受力分析有:
TB-TAsinθ=ma2
TAcosθ=mg
联立解得TA=
,TB=ma2+mgtanθ.mg cosθ
答:(1)车厢静止时,细绳A和B所受的拉力分别为:TA=
,TB=mgtanθ.mg cosθ
(2)车厢的加速度a1的大小为gtanθ,方向水平向右.
(3))若车厢向左以加速度a2匀加速运动时,求A、B两绳拉力的大小分别为TA=
,TB=ma2+mgtanθ.mg cosθ
