问题
问答题
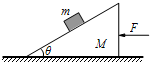
如图所示,光滑斜面体的质量为M,斜角为θ.放置在光滑水平面上,要使质量为m 的物体能静止在光滑斜面体上,应对光滑斜面体施以多大的水平外力F?此时m 与 M 之间的相互作用力 N 为多大?
答案
根据题意要使质量为m 的物体能静止在光滑斜面体上,
则m与M所组成的系统在光滑水平面上有相同的加速度a,对系统受力分析:
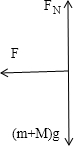
由受力分析图和牛顿第二定律,有:F合=F=(M+m)a.
要求 m 与 M 之间的相互作用力 N,先将 m 从系统中隔离出来,
并对m进行正确的受力分析如图所示,
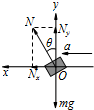
建立如图所示的直角坐标,
将 m 与 M 之间的相互作用力进行正交分解,m在y方向为平衡状态,在x方向为加速状态.
即其 x方向的动力学方程和 y 方向的平衡方程分别为:
y:Ny-mg=0 即 Ncosθ-mg=0
解得:N=mg cosθ
x:F合=Nx=ma 即 Nsinθ=ma
解得a=gtanθ
联立上述方程,解得 F=(M+m)gtanθ.
答:对光滑斜面体施以水平外力F为(M+m)gtanθ,m 与 M 之间的相互作用力 N 为
.mg cosθ
