（1）受力分析如图，将F_N1与F_N2合成，其合力与重力等大反向，利用直角三角形边角关系得：

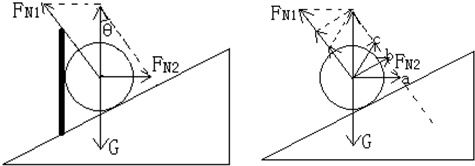
F_N1sinθ=F_N2

F_N1cosθ=G

解得：F_N1=

G

cosθ

；F_N2=Gtanθ

（2）挡板转动时，挡板给球的弹力F_N2与斜面给球的弹力F_N1合力大小方向不变，其中F_N1的方向不变，作辅助图如上，挡板转动过程中，F_N2的方向变化如图中a、b、c的规律变化，为满足平行四边形定则，其大小变化规律为先变小后变大，其中挡板与斜面垂直时为最小．与此对应，F_N1的大小为一直减小．

综上所述，再根据牛顿第三定律得，在该过程中，球对斜面的压力方向垂直斜面指向斜面不变，大小始终减小．球对挡板的压力方向始终与挡板垂直指向挡板，大小先变小后变大．

答：（1）斜面对球的支持力的大小是

G

cosθ

，竖直的挡板对球的弹力是Gtanθ；

（2）若将挡板从竖直位置沿逆时针缓慢旋转至水平位置的过程中，球对斜面的压力方向垂直斜面指向斜面不变，大小始终减小；球对挡板的压力方向始终与挡板垂直指向挡板，大小先变小后变大．