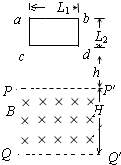
位于竖直平面内的矩形平面导线框abdc,ab长L1=1.0m,bd长L2=0.5m,线框的质量m=0.2kg,电阻R=2Ω.其下方有一匀强磁场区域,该区域的上、下边界PP′和QQ′均与ab平行,两边界间距离为H,H>L2,磁场的磁感应强度B=1.0T,方向与线框平面垂直.如图所示,令线框的dc边从离磁场区域的上边界PP′的距离为h=0.7m处自由下落,已知在线框的dc边进入磁场以后,ab边到达边界PP′之前的某一时刻线框的速度已达到这一阶段的最大值.试求:
(1)线框在ab边到达PP′之前的最大速度
(2)从线框开始下落到dc边刚刚到达磁场区域下边界QQ′的过程中,磁场作用于
线框的安培力做的总功(取g=10m/s2)
(1)设线框进入磁场的过程中最大速度为v0,达到最大速度时:
mg=BIL1=B2
v0L 21 R
则 v0=
=4m/smgR B2 L 21
(2)从达到最大速度到线框的ab到达磁场的上边界PP′,线框的速度保持v0不变,故从线框自由下落至ab边进入磁场的过程中,由动能定理得:
mg(h+L2)+W安=
m1 2 v 20
所以,W安=
m1 2
-mg(h+L2)=-0.8Jv 20
ab边进入磁场后,直到dc边到达磁场下边界QQ′的过程中,线框只在重力作用下做匀加速运动,磁通量不变,没有感应电流产生,整个线框的安培力为零,安培力做功也为零,故从开始下落到dc边刚到达磁场区域下边界QQ′的过程中,安培力做的总功即为线框自由下落至ab边进入磁场的过程中安培力所做的功即:W安=-0.8J
答:
(1)线框在ab边到达PP′之前的最大速度为4m/s.
(2)从线框开始下落到dc边刚刚到达磁场区域下边界QQ′的过程中,磁场作用于线框的安培力做的总功为-0.8J.
