问题
问答题
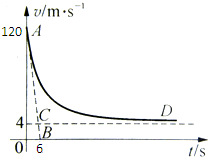
“神舟五号”返回地球,穿越大气层后,在一定的高度打开阻力降落伞进一步减速下降,这一过程中若返回舱所受的空气阻力与速度的平方成正比(设比例系数为k),所受空气浮力恒定不变,且认为返回舱竖直降落.从某时刻开始计时,返回舱运动的v~t图象如图中的AD曲线所示,图中AB是曲线在A点的切线,切线交于横轴上一点B,其坐标为(6,0),CD是曲线AD的渐近线,假如返回舱的总质量M=400kg,g取10
m/s2,试问:
(1)开始计时时返回舱的加速度多大?
(2)在这一阶段返回舱所受的浮力多大?(保留到整数)
答案
(1)零时刻的加速度等于AB直线的斜率,故
a=
=20m/s2 120-0 6
即开始计时时返回舱的加速度大小为20m/s2.
(2)在A点返回舱受到重力、浮力和空气阻力,根据牛顿第二定律,有
k
+F浮-Mg=Ma…①v 20
当以最大速度匀速行驶时,有
k
+F浮-Mg=0…②v 2m
由①式和②式得
F浮=Mg
-M(a+g)v 20 v 2m
-v 20 v 2m
F浮=400×10×1202-400×(20+10)×16 1202-42
F浮≈3991N
即在这一阶段返回舱所受的浮力为3991N.
