问题
填空题
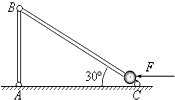
如图所示,AB、BC均为轻杆,处在同一竖直平面内,AB杆高为h. A、B、C三处均用铰接连接,其中A、C两点在同一水平面上,BC杆与水平面夹角为30°.一个质量为m的小球穿在BC杆上,并静止在BC杆底端C处,不计一切摩擦.现在对小球施加一个水平向左的恒力F=
mg,则当小球运动到BC杆的中点时,它的速度大小为______,此时AB杆对B处铰链的作用力大小为______.3
答案
对小球进行受力分析,如图所示:
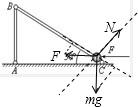
根据牛顿第二定律得:
ma=Fcos30°-mgsin30°=mg
所以a=g
则当小球运动到BC杆的中点时,运动的位移为:
•h sin30°
=h1 2
根据匀加速直线运动位移速度公式得:v=
=2ax 2gh
当小球运动到BC杆的中点时,小球对杆子的作用力方向垂直于杆子向下,根据几何关系得大小:N=mgcos30°=
mg3 2
此时BC杆相当于绕C点转动的杠杆,根据杠杆平衡原理得:
FABlBC=N•
lBC+F•1 2
lAB1 2
解得:FAB=mg
故答案为:
,mg2gh
