问题
填空题
设lg√x,1/2,lgy成等比数列,且x>1,y>1,则xy的最小值是().
答案
参考答案:10√2
解析:
因为lg
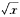 ·lgy=
·lgy=
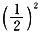 ,得lgx·lgy=
,得lgx·lgy=
 又x>1,y>1,可知 lgx>0,lgy>0,所以 lgx+lgy≥
又x>1,y>1,可知 lgx>0,lgy>0,所以 lgx+lgy≥
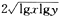 =
=
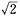 即lgxy≥
即lgxy≥
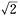 .由此可得xy≥
.由此可得xy≥
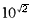 等号仅当x=y时成立.
等号仅当x=y时成立.
设lg√x,1/2,lgy成等比数列,且x>1,y>1,则xy的最小值是().
参考答案:10√2
解析:
因为lg
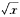 ·lgy=
·lgy=
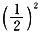 ,得lgx·lgy=
,得lgx·lgy=
 又x>1,y>1,可知 lgx>0,lgy>0,所以 lgx+lgy≥
又x>1,y>1,可知 lgx>0,lgy>0,所以 lgx+lgy≥
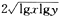 =
=
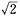 即lgxy≥
即lgxy≥
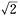 .由此可得xy≥
.由此可得xy≥
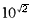 等号仅当x=y时成立.
等号仅当x=y时成立.