如图所示,一质量M=1.0kg的砂摆,用轻绳悬于天花板上O点。另有一玩具枪能连续发射质量m=0.01kg、速度v=4.0m/s的小钢珠。现将砂摆拉离平衡位置,由高h=0.20m处无初速度释放,恰在砂摆向右摆到最低点时,玩具枪发射的第一颗小钢珠水平向左射入砂摆,二者在极短时间内达到共同速度。不计空气阻力,取g =10m/s2。
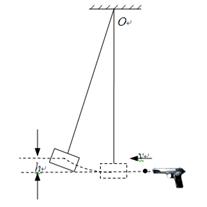
(1)求第一颗小钢珠射入砂摆前的瞬间,砂摆的速度大小v0;
(2)求第一颗小钢珠射入砂摆后的瞬间,砂摆的速度大小v1;
(3)第一颗小钢珠射入后,每当砂摆向左运动到最低点时,都有一颗同样的小钢珠水平向左射入砂摆,并留在砂摆中。当第n颗小钢珠射入后,砂摆能达到初始释放的高度h,求n。
(1)2.0m/s(2)1.94m/s (3)4
题目分析:(1)砂摆从释放到最低点,由动能定理:
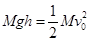
解得: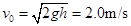
(2)小钢球打入砂摆过程,由动量守恒定律,以右为正方向
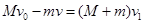
解得: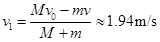
(3)第2颗小钢球打入过程,由动量守恒定律,以左为正方向
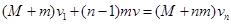
第3颗小钢球打入过程,同理

第n颗小钢球打入过程,同理
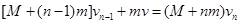
联立各式得: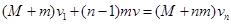
解得: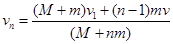
当第n颗小钢球射入后,砂摆要能达到初始释放的位置,
砂摆速度满足: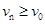
解得: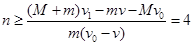
所以,当第4颗小钢球射入砂摆后,砂摆能达到初始释放的高度。
点评:动量守恒和机械能守恒结合的题是常见问题,本题还是多过程问题,要用归纳法列表达式求解。
