问题
证明题
菱形ABCD中，AE⊥BC于E，AF⊥CD于F，求证：AE=AF。
答案
证明：∵AE⊥BC于E，AF⊥CD于F，
∴∠AEB=∠AFD=90°，
∵菱形ABCD，
∴AB=AD，∠B=∠D，
在Rt△EBA和Rt△FDA中，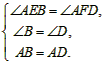
∴△EBA≌△FDA，
∴AE=AF。
搜题请搜索小程序“爱下问搜题”
菱形ABCD中，AE⊥BC于E，AF⊥CD于F，求证：AE=AF。
证明：∵AE⊥BC于E，AF⊥CD于F，
∴∠AEB=∠AFD=90°，
∵菱形ABCD，
∴AB=AD，∠B=∠D，
在Rt△EBA和Rt△FDA中，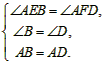
∴△EBA≌△FDA，
∴AE=AF。