问题
填空题
在平行四边形ABCD中,若AC=2且
|
答案
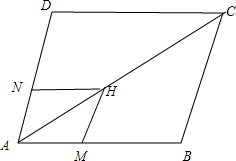
(如图)在平行四边形ABCD中,AC=2,
设
=AM
为AB边上的单位向量,AB |
|AB
=AN
为AC边上的单位向量,且AD |
|AD
+AB |AB|
=AD |
|AD 3 2
=AC
,AH
故AC是∠BAD的平分线,四边形ABCD和AMHN均为菱形,且相似.
由题意可得AH=
AC=3 2
,AB=AD=3 2 3
设向量
与AB
的夹角大小为θ,在菱形AMHN中,∠AMH=π-θ,AH=AD
AC=3 2
,3
△AMH中,由余弦定理可得 3=1+1-2×1×1cos(π-θ)=2+2cosθ,解得 cosθ=
,1 2
故
•AB
=AB×ADcosθ=AD 2 3
故答案为:2 3