问题
解答题
我们知道,若两个有理数的积是1,则称这两个有理数互为倒数.同样的当两个实数(a+
(1)判断(4+
(2)若实数(
|
答案
(1)不互为倒数,
理由如下:∵(4+
)×(4-2
)=16-2=14≠1,2
∴(4+
)与(4-2
)不互为倒数;2
(2)∵(
+x
)与(y
-x
)互为倒数,y
∴(
+x
)×(y
-x
)=1,y
∴x-y=1,
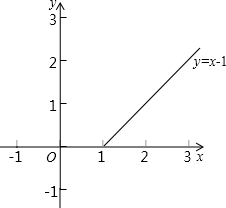
y=x-1,
函数图象如图所示.