问题
计算题
如图所示,N=50匝的矩形线圈abcd,边长ab=20 cm,ad=25 cm,放在磁感应强度B=0.4 T的匀强磁场中,外力使线圈绕垂直于磁感线且通过线圈中线的OO′轴以n=3000 r/min的转速匀速转动,线圈电阻r=1 Ω,外电路电阻R=9 Ω,t=0时,线圈平面与磁感线平行,ab边正转出纸外、cd边转入纸里.
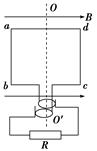
(1)在图中标出t=0时感应电流的方向;
(2)写出线圈感应电动势的瞬时表达式;
(3)从图示位置转过90°过程中流过电阻R的电荷量是多大?
答案
(1) a→d→c→b→a(2) e=314cos100πt V. (3) 0.1 C.
题目分析:(1)根据ab、cd切割磁感线,由右手定则可得线圈中感应电流方向a→d→c→b→a. (2分)
(2)线圈的角速度
ω=2πn=100π rad/s. (2分)
设ab边在t=0时刻速度为vab,图示位置的感应电动势最大,其大小为
Em=2NB·vab=NB··ω=314 V (2分)
电动势的瞬时表达式为:e=314cos100πt V. (2分)
(3)q=IΔt.
从t=0起转过90°的过程中,Δt时间内流过R的电荷量
q= Δt=0.1 C. (4分)
Δt=0.1 C. (4分)
点评:本题难度较小,对于交流电问题要掌握瞬时值、有效值、平均值和最大值的计算方法,求解电荷量问题时要用平均值
