问题
单项选择题
已知
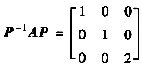，若α1，α2是矩阵A属于特征值λ=1的线性无关的特征向量，α3是矩阵A属于特征值λ=2的特征向量，则矩阵P不能是
答案
参考答案：D
解析：
[分析]： 如Aα=λα，则A(kα)=λ(kα)，即若α是A属于特征值λ的特征向量，则kα(k≠0)仍是矩阵A属于特征值λ的特征向量．
如Aα1=λα1，Aα2=λα2，则A(k1α1+k2α2)=λ(k1α1+k2α2)，即若α1，α2是A属于特征值λ的特征向量，则k1α1+k2α2(非零时)仍是A属于特征值λ的特征向量．
注意，如Aα1=λ1α1，Aα2=λ2α2，λ1≠λ2，则α1+α2，α1-α2等都不是矩阵A的特征向量．
所以(A)，(B)，(C)均正确，唯(D)中α2+α3不再是矩阵A的特征向量，故(D)不正确，应选(D)．
评注 矩阵P中特征向量的顺序要与对角矩阵中特征值的顺序相一致.在本题中，如若令P=(α3,α2,α1)，则也是错误的，(B)之所以正确是因为α1,α2都是A属于特征值λ=1的特征向量.