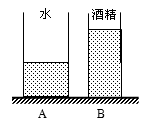
如图所示，质量均为2.4kg的薄壁圆柱形容器A和B放在水平地面上，底面积分别为
和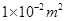
。容器A中盛有0.1m高的水，容器B中盛有质量为1.6kg的酒精。（ρ酒精＝0.8×103kg/m3）求：
①容器B中酒精的体积V酒精。
②容器B对水平地面的压强pB。
③现有质量相等的甲、乙两实心物块，若将甲浸没在水中、乙浸没在酒精中后，两液体均未溢出，且两液体各自对容器底部压强的变化量相等，求甲、乙的密度ρ甲、ρ乙之比。
(1) 2×10-3m3, (2) 3920pa, (3) ρ甲：ρ乙＝5:8
题目分析：(1)已知酒精的质量和密度，要求酒精的体积，可利用公式V＝m/ρ求出，
V酒精＝m酒精/ρ酒精＝1.6kg/0.8×103kg/m3＝2×10-3m3
(2)容器B对水平地面的压强可利用公式P＝F/S求出，已知容器B的底面积，要先求出容器B对水平地面的压力，而容器B对水平地面的压力是由重力产生的，所以压力等于总重力（G容器+G酒精）
FB＝G总＝m总g＝（m酒精+mB）g＝（2.4kg＋1.6kg）×9.8N/kg＝39.2N
pB＝FB/SB ＝39.2N/1×10－2m2＝3920pa
(3)两液体各自对容器底部压强的变化量相等,即：Dp水＝Dp酒精
由液体压强的计算公式P＝ρgh可得：
ρ水gDh水＝ρ酒精gDh酒精（Dh水和Dh酒精分别表示放入物体后液面上升的高度）
因为“若将甲浸没在水中、乙浸没在酒精中后，两液体均未溢出”，所以液面上升的高度可用物体排开液体的体积和容器的底面积求出：ρ水gDV水/SA＝ρ酒精gDV酒精/SB
因为浸没，所以排开液体的体积就等于物体的体积：ρ水gV甲/SA＝ρ酒精gV乙/SB
而物体的体积可根据物休的质量和密度求出：ρ水gm甲/（ρ甲SA）＝ρ酒精g m乙/（ρ乙SB）
因为是质量相等的甲、乙两实心物块，所以约分后有：ρ水/（ρ甲SA）＝ρ酒精/（ρ乙SB）
所以：ρ甲：ρ乙＝ρ水SB：ρ酒精SA ＝（1000kg/m3×1×10－2m2）：（0.8×103kg/m3×2×10－2m2）＝5:8
