问题
计算题
如图甲所示，三个物体A、B、C静止放在光滑水平面上，物体A、B用一轻质弹簧连接，并用细线拴连使弹簧处于压缩状态，三个物体的质量分别为mA=0.1kg、mB=0.2kg和mC=0.1kg。现将细线烧断，物体A、B在弹簧弹力作用下做往复运动（运动过程中物体A不会碰到物体C）。若此过程中弹簧始终在弹性限度内，并设以向右为正方向，从细线烧断后开始计时，物体A的速度‒时间图象如图18乙所示。求：
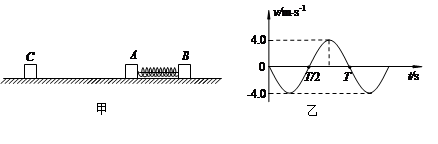
（1）从细线烧断到弹簧恢复原长运动的时间；
（2）弹簧长度最大时弹簧存储的弹性势能；
（3）若弹簧与物体A、B不连接，在某一时刻使物体C以v0的初速度向右运动，它将在弹簧与物体分离后和物体A发生碰撞，所有碰撞都为完全弹性碰撞，试求在以后的运动过程中，物体C与物体A能够发生二次碰撞，物体C初速度v0的取值范围。（弹簧与物体分离后，迅速取走，不影响物体后面的运动）
答案
：18. (1)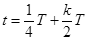 
k =0，1，2…… (2)1.2J (3) v0>20m/s
题目分析：（1）当弹簧恢复到原长时，A的速度最大，
则对应的时刻为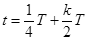 （k =0，1，2……）
（2）当A的最大速度为4m/s,
此时根据动量守恒定律可得B的速度为：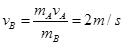
，
AB总的动能即为弹簧长度最大时弹簧存储的弹性势能，
即
;
(3)当A与弹簧分离时的速度为vA=4m/s,
第一次和C碰撞时满足：
,
,
物体C与物体A能够发生二次碰撞,则需满足 
，
联立以上方程解得：v0>20m/s。