问题
证明题
已知四边形ABCD中，AB=CD，E、F分别为AD、BC的中点，BA、CD的延长线分别与FE的延长线交于G、H。
求证：∠BGF=∠CHF。
答案
证明：连结BD，作EK//AB交BD于K，连结KF。
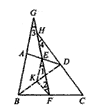
在△DAB中，E为AD中点，EK//AB
所以K为BD中点，
所以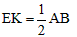
同理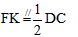
因为AB=CD
所以∠1=∠2
即∠3=∠4
所以∠BGF=∠CHF
搜题请搜索小程序“爱下问搜题”
已知四边形ABCD中，AB=CD，E、F分别为AD、BC的中点，BA、CD的延长线分别与FE的延长线交于G、H。
求证：∠BGF=∠CHF。
证明：连结BD，作EK//AB交BD于K，连结KF。
在△DAB中，E为AD中点，EK//AB
所以K为BD中点，
所以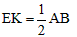
同理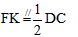
因为AB=CD
所以∠1=∠2
即∠3=∠4
所以∠BGF=∠CHF