问题
解答题
已知命题p:方程
|
答案
∵方程
-x2 2m
=1表示焦点在x轴上的双曲线,y2 m-2
∴
⇒m>22m>0 m-2>0
若p为真时:m>2,
∵曲线y=x2+(2m-3)x+1与x轴交于不同的两点,
则△=(2m-3)2-4>0⇒m>
或m<5 2
,1 2
若q真得:m>
或m<5 2
,1 2
由复合命题真值表得:若p∧q为假命题,p∨q为真命题,p,q命题一真一假
若p真q假:2<m≤
;5 2
若p假q真:m<1 2
∴实数m的取值范围为:2<m≤
或m<5 2
.1 2

 中,a和b的意义是()。
中,a和b的意义是()。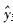 平均变动的数量
平均变动的数量