问题
填空题
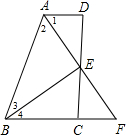
如图:在四边形ABCD中,点E在边CD上,连接AE、BE并延长AE交BC的延长线于点F,给出下 * * 个关系式:①AD∥BC,②DE=EC,③∠1=∠2,④∠3=∠4,⑤AD+BC=AB.将其中三个关系式作为已知,另外两个作为结论,构成正确的命题.请用序号写出两个正确的命题:(书写形式:如果…那么…)(1)______;(2)______.
答案
如果①②③,那么④⑤.理由如下:
∵AD∥BC,
∴∠1=∠F,∠D=∠ECF,
而DE=EC,
∴△AED≌△FEC,
∴AD=CF,
∵∠1=∠2,
∴∠2=∠F,
∴AB=BF,
而BF=BC+CF,
∴AD+BC=AB;
如果①③④,那么②⑤.理由如下:
∵AD∥BC,
∴∠1=∠F,
而∠1=∠2,
∴∠2=∠F,
∴BA=BF,
∵∠3=∠4,
∴BE平分AF,
即AE=EF,
易证△AED≌△FEC,
∴AD=CF,DE=EC,
而BF=BC+CF,
∴AD+BC=AB.
故答案为如果①②③,那么④⑤;如果①③④,那么②⑤.
