已知函数f(x)=sin2x+2sinxcosx+3cos2x
(Ⅰ)求函数f(x)图象的对称中心的坐标;
(Ⅱ)求函数f(x)的最大值,并求函数f(x)取得最大值时x的取值集合;
(Ⅲ)求函数f(x)的增区间
(Ⅰ)f(x)=
(1-cos2x)+sin2x+1 2
(1+cos2x)3 2
=sin2x+cos2x+2=
sin(2x+2
)+2.π 4
令2x+
=kπ得x=π 4
-kπ 2
(k∈Z),π 8
∴函数f(x)图象对称中心的坐标是(
-kπ 2
, 0),(k∈Z).π 8
(Ⅱ)当2x+
=2kπ+π 4
,π 2
即x=kπ+
(k∈Z)时,ymax=2+π 8
.2
∴函数f(x)取得最大值时X的集合是{x|x=kπ+
,k∈Z}.π 8
(Ⅲ)由2kπ-
≤2x+π 2
≤2kπ+π 4
,π 2
得kπ-
≤x≤kπ+3π 8
(k∈Z),π 8
∴函数f(x)的单调增区间是[kπ-
,kπ+3π 8
](k∈Z).π 8

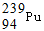
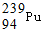 可由铀239(
可由铀239(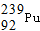
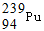 与
与 的核内具有相同的中子数
的核内具有相同的中子数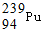 与
与
