问题
解答题
在△ABC中,满足
(1)若|
(2)若|
|
答案
(1)设|
|=1,AB
•AB
=|AC
|•|AB
|cos60°=AC
,1 2
则|
+2AB
|=AC
=|
|2+4AB
⋅AB
+(2AC
)2AC
=1+4×
+41 2 7
而
•(AB
+2AB
)=2,AC
所以向量
+2AB
与AC
的夹角的余弦值等于cosθ=AB
=
⋅(AB
+2AB
)AC |
+2AB
|⋅|AC
|AB
=2 7
.2 7 7
(2)在|
|2=|BC
|2+|AC
|2-2|AB
|•|AB
|•cos60°,AC
解得|
|=4,AC
因为
⊥MD
,所以|AC
|=cos60°=AD
,1 2
故λ=
.1 8

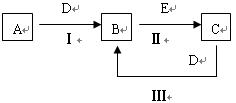
 A是能使湿润的红色试纸变蓝的气体;C、D均为空气的主要成分,E是一种无色无味的有毒气体。①写出E的化学式 ;
A是能使湿润的红色试纸变蓝的气体;C、D均为空气的主要成分,E是一种无色无味的有毒气体。①写出E的化学式 ; 电子粒子
电子粒子 下B是黄绿色气体,C溶液呈碱性,有漂白性。
下B是黄绿色气体,C溶液呈碱性,有漂白性。