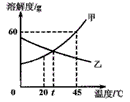
问题
计算题
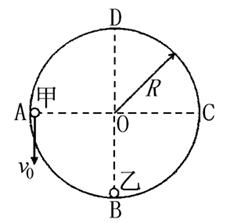
(19分)如图所示,光滑水平面上固定一半径为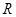 的光滑水平圆形轨道,过圆心
的光滑水平圆形轨道,过圆心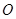 相垂直的两虚线交圆弧于A、B、C、D四点,质量为
相垂直的两虚线交圆弧于A、B、C、D四点,质量为 的乙球静置于B处,质量为
的乙球静置于B处,质量为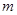 的甲球从A处沿圆弧切线方向以速度
的甲球从A处沿圆弧切线方向以速度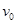 开始运动,到达B处与乙球发生碰撞,碰撞时间很短可忽略不计,碰撞为弹性碰撞,两小球可视为质点.当乙球刚运动到D处时,两小球发生第二次碰撞.求:
开始运动,到达B处与乙球发生碰撞,碰撞时间很短可忽略不计,碰撞为弹性碰撞,两小球可视为质点.当乙球刚运动到D处时,两小球发生第二次碰撞.求:
(1)第一次碰撞前甲所受轨道弹力的大小;
(2)甲、乙两球质量之比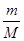 ;
;
(3)甲与乙第二次碰撞后各自速度的大小.
答案
(1)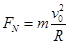 (2)
(2)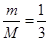 (3)
(3)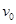 、0
、0
题目分析:(1)甲与乙第一次碰撞前,对甲受力知受重力和轨道的支持力 ,由牛顿第二定律:
,由牛顿第二定律:
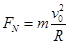 (5分)
(5分)
(2)由题分析知,甲与乙第一次碰撞后必反向运动,速度大小必相等
设甲、乙第一次碰撞后速度大小分别为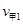 、
、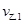 ,以向右为正方向
,以向右为正方向
有: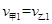 (1分)
(1分)
由动量守恒定律: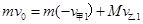 (2分)
(2分)
由能量守恒定律: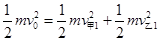 (2分)
(2分)
解得: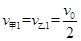 ,
, 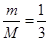 (2分)
(2分)
(3)设甲、乙第二次碰撞后各自速度大小为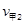 、
、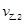 ,
,
由动量守恒定律: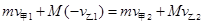 (2分)
(2分)
由能量守恒定律: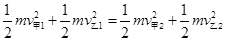 (2分)
(2分)
解得: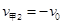
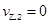
即甲与乙第二次碰撞后各自速度大小分别为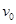 和0 (3分)
和0 (3分)