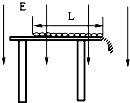
如图所示，有一柔软链条全长为L=1.0m，质量分布均匀，总质量为M=

问题问答题

如图所示，有一柔软链条全长为L=1.0m，质量分布均匀，总质量为M=2.0kg，链条均匀带电，总电荷量为Q=1.0×10^-6C，将链条放在离地足够高的水平桌面上，链条与桌边垂直，且一端刚好在桌边，桌边有光滑弧形挡板，使链条离开桌边后只能竖直向下运动．在水平桌面的上方存在竖直向下的匀强电场，电场强度的大小E=2.0×10⁷V/m．若桌面与链条间的动摩擦因数为μ=0.5（重力加速度取10m/s²），试求：

（1）链条受到的最大滑动摩擦力；

（2）当桌面下的链条多长时，桌面下的链条所受到的重力恰好等于链条受到的滑动摩擦力；

（3）从桌面上滑下全部链条所需的最小初动能．

答案

（1）最大静摩擦力约等于滑动摩擦力，则有：f_max=μ（Mg+QE）=20 N，

（2）设桌面下的链条长为x，链条质量分布均匀，所以在桌面下的链条的质量为

，则有：

g=μ

L-x

（Mg+QE），

解得x=0.5 m，

（3）链条下滑0.5 m后就会自动下滑，此时速度正好为零时所需初动能最小，根据动能定理有：

-W_f=0-E_k0，

由于f和N成正比，N和链条下滑的长度成正比，所以f是均匀变化的．

可以根据平均摩擦力来求W_f

Wf=

f1+f2

•

f₁是最初瞬间的摩擦力，即f_MAX，所以f₁=20N

f₂是下滑0.5m时的摩擦力，由第二问得知，其大小等于半根链条的重力，f₂=10N

解得：E_k0=W_f-

MgL

f1+f2

MgL

=7.5-2.5J=5 J

答：（1）链条受到的最大滑动摩擦力为20N；

（2）当桌面下的链条0.5m时，桌面下的链条所受到的重力恰好等于链条受到的滑动摩擦力；

（3）从桌面上滑下全部链条所需的最小初动能为5J．