问题
计算题
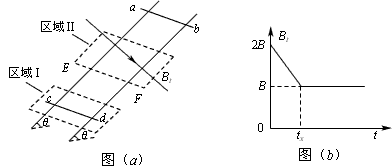
如图（a）所示，间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上。在区域I内有方向垂直于斜面的匀强磁场，磁感应强度恒为B不变；在区域Ⅱ内有垂直于斜面向下的匀强磁场，其磁感应强度Bt的大小随时间t变化的规律如图（b）所示。t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑，同时下端的另一金属细棒cd在位于区域I内的导轨上也由静止释放。在ab棒运动到区域Ⅱ的下边界EF之前，cd棒始终静止不动，两棒均与导轨接触良好。已知cd棒的质量为m、电阻为R，ab棒的质量、阻值均未知，区域Ⅱ沿斜面的长度为l，在t=tx时刻（tx未知）ab棒恰好进入区域Ⅱ，重力加速度为g。求：
（1）区域I内磁场的方向；
（2）通过cd棒中的电流大小和方向；
（3）ab棒开始下滑的位置离区域Ⅱ上边界的距离；
（4）ab棒开始下滑至EF的过程中，回路中产生总的热量。（结果用B、l、θ、m、R、g表示）
答案
解：（1）I内磁场垂直于斜面向上
（2）cd棒平衡，BIl=mgsinθ，I=
电流方向d→c
（3）前、后回路感应电动势不变，
=Blvx，即
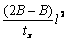=Blvx
解得l=vxtx
ab棒进入区域Ⅱ之前不受磁场力的作用，做匀加速直线运动
S1=
(0+v)tx=0.5l
（4）ab棒进入区域Ⅱ后作匀速直线运动，t2=tx，总时间t总=tx+t2=2tx
电动势E=Blvx不变
总热量：Q=EIt总=2mgvxtxsinθ=2mglsinθ