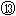如图所示，在距离水平地面h＝0.8 m的虚线的上方，有一个方向垂直于纸面水平向内的匀强磁场。正方形线框abcd的边长l＝0.2 m，质量m＝0.1 kg，电阻R＝0.08 Ω。一条不可伸长的轻绳绕过轻滑轮，一端连线框，另一端连一质量M＝0.2 kg的物体A。开始时线框的cd在地面上，各段绳都处于伸直状态，从如图所示的位置由静止释放物体A，一段时间后线框进入磁场运动，已知线框的ab边刚进入磁场时线框恰好做匀速运动。当线框的cd边进入磁场时物体A恰好落地，同时将轻绳剪断，线框继续上升一段时间后开始下落，最后落至地面。整个过程线框没有转动，线框平面始终处于纸面内，g取10 m/s2。求：
(1)匀强磁场的磁感应强度B？
(2)线框从开始运动到最高点，用了多长时间？
(3)线框落地时的速度多大？
解：(1)设线框到达磁场边界时速度大小为v，由机械能守恒定律可得：
Mg(h－l)＝mg(h－l)＋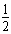
(M＋m)v2 ①
代入数据解得：v＝2 m/s ②
线框的ab边刚进入磁场时，感应电流：I＝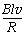
③
线框恰好做匀速运动，有：Mg＝mg＋IBl ④
代入数据解得：B＝1 T ⑤
(2)设线框进入磁场之前运动时间为t1，有：h－l＝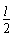
vt1 ⑥
代入数据解得：t1＝0.6 s ⑦
线框进入磁场过程做匀速运动，所用时间：t2＝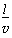
＝0.1 s ⑧
此后轻绳拉力消失，线框做竖直上抛运动，到最高点时所用时间：t3＝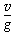
＝0.2 s ⑨
线框从开始运动到最高点，所用时间：t＝t1＋t2＋t3＝0.9 s ⑩
(3)线框从最高点下落至磁场边界时速度大小不变，线框所受安培力大小也不变，即
IBl＝(M－m)g＝mg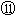 
因此，线框穿过磁场过程还是做匀速运动，离开磁场后做竖直下抛运动．由机械能守恒定律可得：
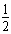mv12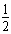＝mv2＋mg(h－l) 
代入数据解得线框落地时的速度：v1＝4 m/s 