问题
计算题
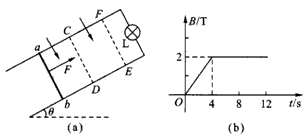
如图(a)所示,固定在倾斜面上电阻不计的金属导轨,间距d=0.5 m,斜面倾角θ=37°,导轨上端连接一阻值为R=4 Ω的小灯泡L。在CDEF矩形区域内有垂直于斜面向下的匀强磁场,磁感应强度B随时间t变化的规律如图(b)所示,CF长为2m。开始时电阻为1 Ω的金属棒ab放在斜面导轨上刚好静止不动,在t=0时刻,金属棒在平行斜面的恒力F作用下,由静止开始沿导轨向上运动。金属棒从图中位置运动到EF位置的整个过程中,小灯泡的亮度始终没有发生变化。设最大静摩擦力与滑动摩擦力相等,g=10 m/s2,sin37°=0.6,cos37°=0.8。求:
(1)通过小灯泡的电流强度;
(2)恒力F的大小、金属棒与导轨间的动摩擦因数和金属棒的质量。
答案
解:(1)金属棒未进入磁场时,电路总电阻R总=R+Rab=5Ω
回路中感应电动势为: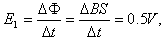
灯泡中的电流强度为: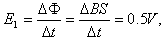
(2)因灯泡亮度不变,故在t=4 s末金属棒刚好进入磁场,且做匀速运动,此时金属棒中的电流强度:I=IL=0.1 A
又因为开始时电阻为1 Ω的金属棒放在斜面导轨上刚好静止不动
mgsinθ=μmgcosθ,μ=tanθ=0.75
恒力大小:F=F安+2mgsinθ=BId+2mgsinθ=0.1+12m
因灯泡亮度不变,金属棒产生的感应电动势为:E2=E1=0.5 V
金属棒在磁场中的速度: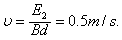
金属棒未进入磁场的加速度为:
根据牛顿第二定律得:F-2mgsinθ=ma
联立解得m=0.8 kg,F=9.7 N
