问题
计算题
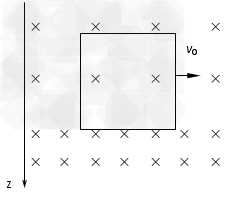
如图所示,竖直平面内有一边长为L、质量为m、电阻为R的正方形线框在竖直向下的重力场和水平方向的匀强磁场组成的复合场中以速度v0水平抛出,磁场的方向与线框平面垂直,磁场的磁感应强度随竖直向下的z轴按B=B0+kz的规律均匀增大,已知重力加速度为g,求:
(1)线框竖直方向速度为v1时,线框中瞬时电流的大小I;
(2)线框在复合场中运动时重力的最大电功率Pm;
(3)若线框从开始抛出到瞬时速度大小达到v2所经历的时间为t,那么,线框在时间t内的竖直方向位移大小z。
答案
解:(1)左右两边产生的感应电动势抵消,设线框上下边处的磁感应强度分别为B1和B2,有
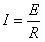
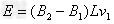
得 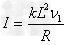
(2)当安培力大小等于重力时竖直速度最大,重力的功率也最大
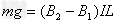
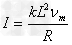
所以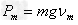
得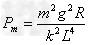
(3)线框受重力和安培力作用,其中重力为恒力,安培力为变力。设某时刻线框竖直方向的速度为vz,则安培力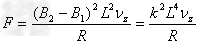
设在微小△t内,变力可以看做匀加速运动,由牛顿第二定律线框加速度为
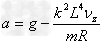
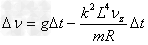
所以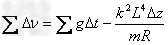
有
解得