问题
计算题
（13分）如图所示，在光滑的水平面上有一长为L的木板B，上表面粗糙，在其左端有一光滑的1/4圆弧槽C，与长木板接触但不相连，圆弧槽的下端与木板上表面相平，B、C静止在水平面上。现有滑块A以初速v0从右端滑上B，一段时间后，以v0/2滑离B，并恰好能到达C的最高点。A、B、C的质量均为m。求：
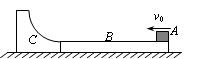
⑴A刚滑离木板B时，木板B的速度；
⑵A与B的上表面间的动摩擦因数μ；
⑶圆弧槽C的半径R；
⑷从开始滑上B到最后滑离C的过程中A损失的机械能。
答案
⑴v0/4 ⑵5v02/16gL （3）v02/64g（4）15mv02/32
题目分析：（1）对A在长木板B上的滑动过程，取ABC为一个系统，根据动量守恒定律有：
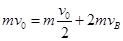解得
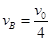
(2) 对A在长木板B上的滑动过程,ABC系统动能减少全部转化为系统的摩擦生热
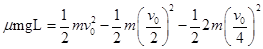
解得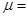
5v02/16gL
⑶对A滑上C直到最高点的作用过程，AC系统动量守恒，mv0/2+mvB=2mv①
AC系统机械能守恒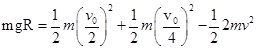
②
①②联立得R= v02/64g
⑷对A滑上C直到离开C的作用过程,AC系统动量守恒mv0/2+mv0/4=mvA+mvC①
AC系统初、末状态动能相等，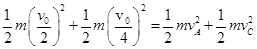
②
①②联立解得vA=v0/4。
所以从开始滑上B到最后滑离C的过程中A损失的机械能为：
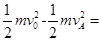15mv02/32