问题
计算题
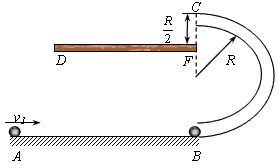
如图所示，一质量m1=0.2kg的小球，从光滑水平轨道上的一端A处，以v1=2.5m/s的速度水平向右运动。轨道的另一端B处固定放置一竖直光滑半圆环轨道（圆环半径比细管的内径大得多），轨道的半径R=10cm，圆环轨道的最低点与水平轨道相切；空中有一固定长为15cm的木板DF，F端在轨道最高点C的正下方，竖直距离为5cm。水平轨道的另一端B处有一质量m2=0.2kg的小球，m1、m2两小球在B处发生的是完全弹性碰撞，重力加速度为g=10m/s2。求：
（1）经过C点时，小球m2对轨道的作用力的大小及方向？
（2）m2小球打到木板DF上的位置？
答案
解：（1）在B处m1与m2发生的是完全弹性碰撞，有：
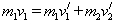①
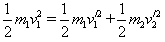②
由①②式解得：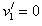
，
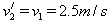
（或因m1与m2发生的是完全弹性碰撞，且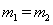
，所以两球交换速度。得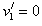
）
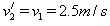由B到C的过程，机械能守恒，有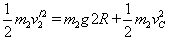
③
由③代入数据得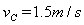
在C点，对m2根据牛顿第二定律：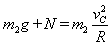
④
由④代入数据得：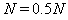
，方向竖直向下
据牛顿第三定律知：小球对轨道的作用力大小为0.5N，方向竖直向上
（2）小球从C飞出做平抛运动，有
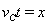⑤
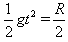⑥
由⑤⑥解得：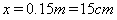
，所以物体刚好落在木板的D点上
