（10分）如图甲所示，三个物体A、B、C静止放在光滑水平面上，物体A、B用一轻质弹簧连接，并用细线拴连使弹簧处于压缩状态，此时弹簧长度L=0.1m；三个物体的质量分别为mA=0.1kg、mB=0.2kg和mC=0.1kg。现将细线烧断，物体A、B在弹簧弹力作用下做往复运动（运动过程中物体A不会碰到物体C）。若此过程中弹簧始终在弹性限度内，并设以向右为正方向，从细线烧断后开始计时，物体A的速度‒时间图象如图18乙所示。求：
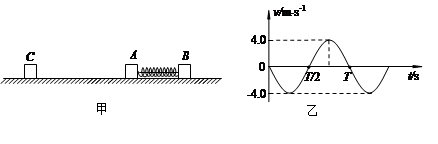
（1）物体B运动速度的最大值；
（2）从细线烧断到弹簧第一次伸长到L1=0.4m时，物体B运动的位移大小；
（3）若在某时刻使物体C以vC=4m/s的速度向右运动，它将与正在做往复运动的物体A发生碰撞，并立即结合在一起，试求在以后的运动过程中，弹簧可能具有的最大弹性势能的取值范围。
（1）2m/s（2）xB=0.1m（3）0.2J≤Epm<1.8J
题目分析：（1）对于物体A、B与轻质弹簧组成的系统，当烧断细线后动量守恒，设物体B运动的最大速度为vB，有
mAvA+mBvB=0
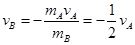
由图乙可知，当t=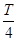
时，物体A的速度vA达到最大，vA=-4m/s
则vB=2m/s
即物体B运动的最大速度为2m/s （2分）
（2）设A、B的位移大小分别为xA、xB，瞬时速度的大小分别为v¢A、v¢B
由于系统动量守恒，则在任何时刻有 mAv¢A-mBv¢B="0"
则在极短的时间Δt内有 mAv¢AΔt-mBv¢BΔt=0
mAv¢AΔt=mBv¢BΔt
累加求和得： mA∑v¢AΔt=mB∑v¢BΔt
mAxA=mBxB
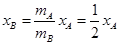
依题意 xA+xB=L1- L
解得 xB=0.1m （4分）
（3）因水平方向系统不受外力，故系统动量守恒，因此，不论A、C两物体何时何处相碰，三物体速度相同时的速度是一个定值，总动能也是一个定值，且三个物体速度相同时具有最大弹性势能。
设三个物体速度相同时的速度为v共
依据动量守恒定律有mCvC=（mA＋mB＋mC）v共，解得v共 ＝1m/s
当A在运动过程中速度为4m/s且与C同向时，跟C相碰，A、C相碰后速度v1= vA= vC，设此过程中具有的最大弹性势能为E1
由能量守恒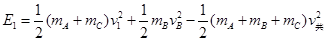 
=1.8J
当A在运动过程中速度为-4m/s时，跟C相碰，设A、C相碰后速度为v2，由动量守恒
mC vC–mA vA＝（mA + mC）v2， 解得v2=0
设此过程中具有的最大弹性势能设为E2
由能量守恒
＝0.2J
由上可得：弹簧具有的最大弹性势能Epm的可能值的范围：0.2J≤Epm<1.8J。（4分）
说明：计算题中用其他方法计算正确同样得分。